Huff By Example

In this rapidly evolving landscape of blockchain technology, efficiency isn't just an advantage—it's a necessity. More the adoption is, the more congested the networks become (for now this is the case), hence the race for gas optimization intensifies, every opcode, every byte, and every operation counts. Enter Huff, a language so close to the metal of the Ethereum Virtual Machine (EVM) which has the potential to take on-chain possibilities to one step further.

In this post, we’ll dive into the basics of Huff by solving one of the Huff Puzzles created by RareSkills. Whether you're a seasoned smart contract developer or a curious newcomer aiming to push the boundaries of what's possible in smart contract optimization, (I hope) this article serves as a guide to strengthen your Huff and EVM fundamentals.

So grab a cup of coffee, and let's get started with this walkthrough!

Background

Huff is a domain-specific low level EVM programming language created in 2019 by Zac Willamson and team (Aztec protocol) to efficiently implement a form of elliptic curve multiplication library called weierstrudel.

Weistrudel is a ECC library  that helps to perform elliptic curve scalar multiplication on the short Weierstrass 254-bit Barreto-Naehrig curve. The contract will multiply up to 15 elliptic curve points with up to 15 different scalars.

Since operations performed on elliptic curves can get quite complex, they cannot be often executed on-chain due the block’s gaslimit constraints. So Zac came up with a new language, Huff, to implement the library.

In general, Huff removes away all the abstraction provided by Solidity and grants a more granular level control over EVM even more than Yul which makes the resulting bytecode more optimized and efficient in terms of both size and gas consumption. Due to this reason, the adoption of Huff grew and people started to build their own optimized version of libraries and smart contracts.

Currently, Huff is completely open-source and is maintained by the community. Also the core developers recently migrated the entire Huff compiler implementation to Rust which is a great leap.

Okay, I think this is enough introduction to understand the need for having a separate language to write smart contracts. If you’re interested in reading more about Huff background, I recommend this medium post written by Zac himself.

Huff syntax

Before diving into loops, I’ll give a quick intro to the basic Huff syntax, which is quite unique: no variables, no operators and no types.

You can define your logic as macros or functions and plug it inside a jump table (function dispatcher). The function dispatcher is usually the MAIN() macro which transfers control to specific macros and functions based on the function selector.

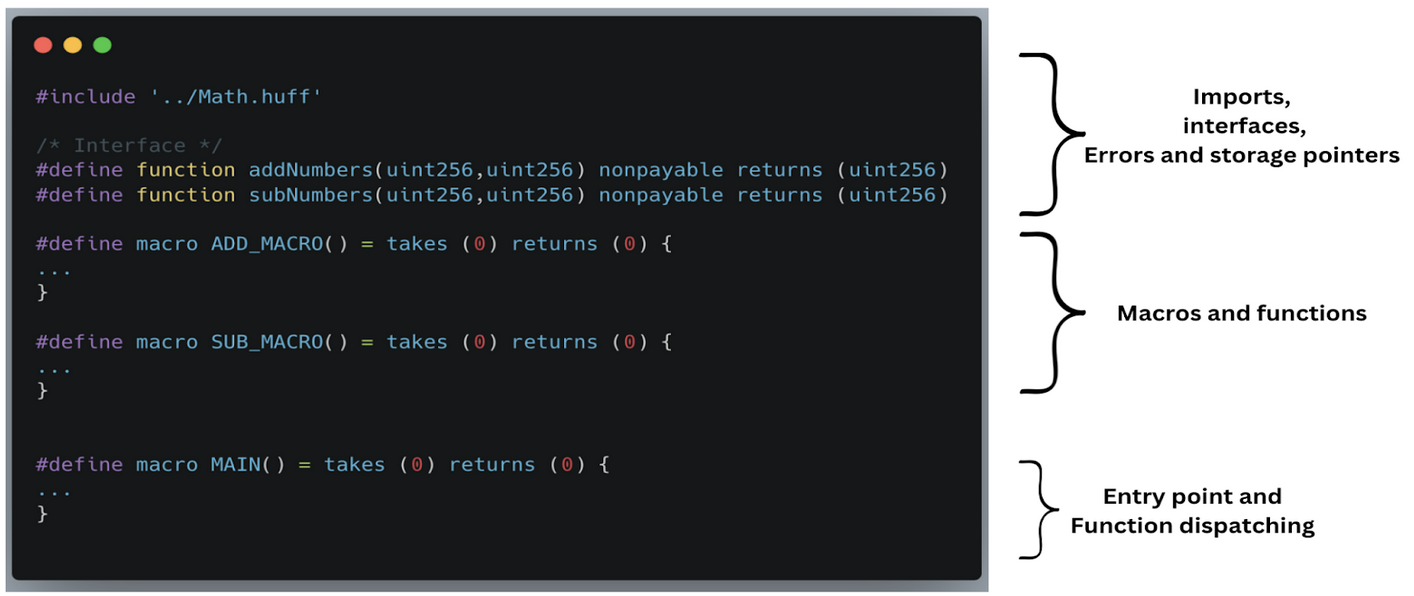
Basic Huff contract structure

The Puzzle

There are several puzzles in the `huff-puzzles` repo. It is an awesome repo with challenges of various levels that could help you get better at Huff. Today, we’ll look into the `SumArray`  challenge which is all about implementing a contract in Huff with a function to accept an unsigned integer array (uint256), sum all the elements and return the sum.

The stub for the puzzle is given in the challenge contract:

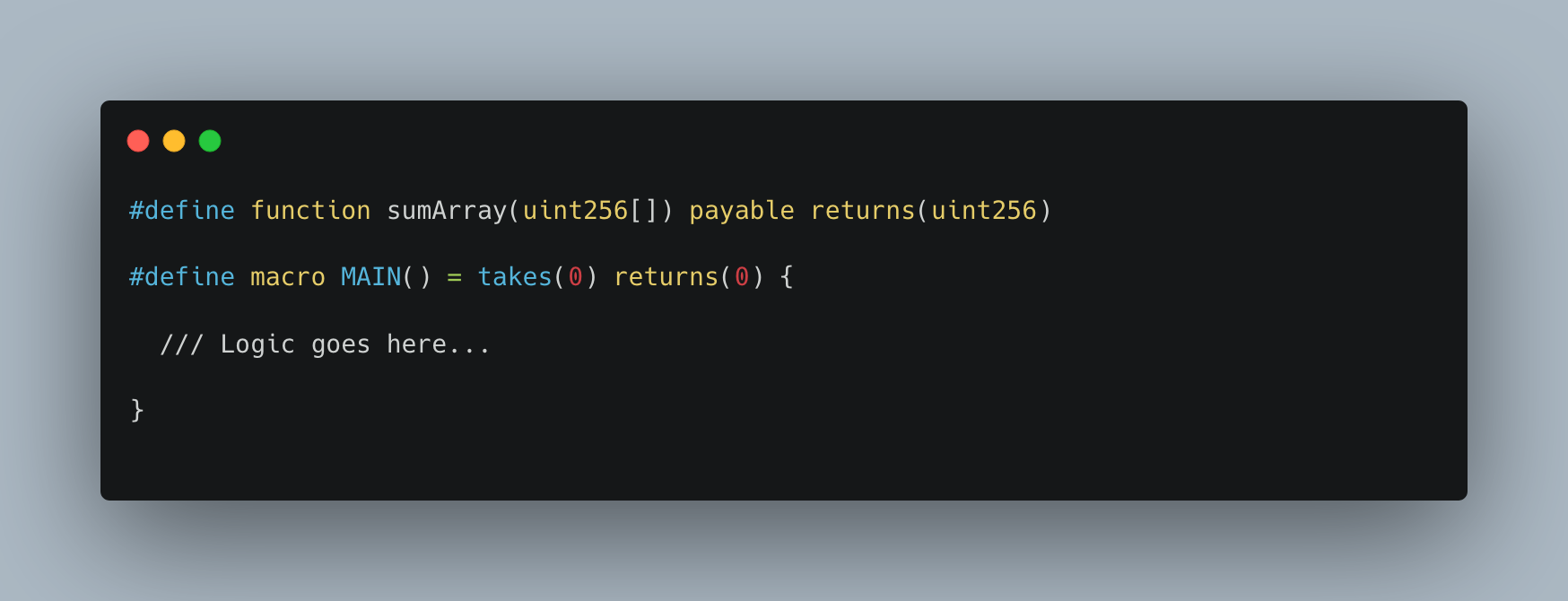
Goal: Our implementation should satisfy the testcases defined in `SumArray.t.sol`

High-level Solution

Before diving into the Huff solution, let’s do a quick reference implementation of our solution in a high-level language like Solidity. The solution contract would look like something like this:

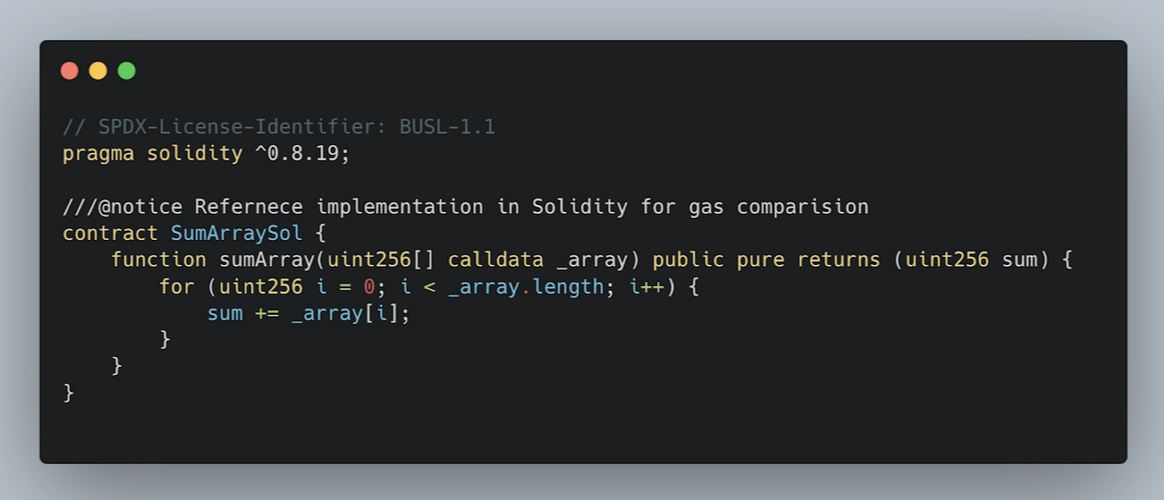
Even though the above contract looks very simple, solidity handles a lot for us under the hood like bound check, offset calculation, calldata slicing, stack manipulation and more.

Let’s break it down.

• Bound checking: Everytime when we try to access an array element via indexing (_array[i]), the solc (solidity compiler) checks if the index i, is less than the array size. If not, it throws an Out-of-bounds exception.

• Offset calculation: Offset calculation is required to calculate the position of the array elements which is required for retrieval by slicing the data from memory or calldata.

• Stack manipulation: EVM is a stack based VM, so every operation is based on the stack operations like PUSH, POP, SWAP, DUP, etc.,. Solidity handles this for us under the hood.

Huff Solution

We’ll be now converting the above reference implementation to Huff to solve this puzzle. Here’s the full solution if you wanna have a peek:

Let’s go through the SUM_ARRAY() macro which handles all the logic with a sample input. Sample input: [1,3, 5] Expected output: 9 In EVM, everything is encoded into bytes. So there’s no difference between various types. It’s the solidity compiler which has all the type definitions and does all the heavy lifting to process the inputs and outputs for operations. So when we make a call to our Huff contract (sumArray(uint256[])) method with the above sample array as in input the calldata would be something like:

0x1e2aea0600000000000000000000000000000000000000000000000000000000000000200000000000000000000000000000000000000000000000000000000000000003000000000000000000000000000000000000000000000000000000000000000100000000000000000000000000000000000000000000000000000000000000030000000000000000000000000000000000000000000000000000000000000005

You can generate the above calldata in solidity with below piece of code:

bytes memory _calldata = abi.encodeWithSignature(“sumArray(uint256[])”, inputArray);

The first 4 bytes is the function selector: 0x1e2aea06 is the function selector which will be used to pass control where the logic for the function resides. Next there is a 32 byte padded value: 0x20 which translates to 32 indicating the offset for every array element. Then the next 32 byte padded value: 0x3 indicates the number of array elements. Followed by 3, 32 byte padded values 1, 2 and 5, which is the input array. To read more about the function selector and argument encoding, I recommend the ABI Spec from Solidity docs: https://docs.soliditylang.org/en/v0.8.21/abi-spec.html# The MAIN() macro:

#define macro MAIN() = takes(0) returns(0) { // Identify which function is being called. 0x00 calldataload // Extract the function singature 0xe0 shr // Jump table dup1 __FUNC_SIG(sumArray) eq sumArray jumpi // Revert if the selector doesn't match 0x00 0x00 revert sumArray: SUM_ARRAY() }

This is the entry point and it acts as the function dispatcher. It receives the calldata, right shifts the data by 224 bits to the right to extract the function selector. Then we check if the input signature matches one of the functions signature, in this case its sumArray. If it matches, the control will be passed to the SUM_ARRAY() macro, otherwise the call will be reverted.

Let’s break down the implementation of SUM_ARRAY() macro for our sample input for 1 iteration:

Initialize Array Length:

0x44 calldatasize sub // [96] array length is 3 * 32

Subtracts 68 (0x44) from the calldata size to get the length of the array, pushing it onto the stack. We subtract 68 because we know the first 4 bytes are for function selector and the remaining 64 bytes are for offset size and array length. Initialize Sum and Index:

push0 // [0, 96] sum=0 push0 // [0, 0, arrayLength] i=0

Push two zeroes onto the stack. The first zero is for the sum accumulator, and the second zero is for the index i.

Loop Start Label

loopBegin:

Define the label loopBegin to jump back to for each iteration of the loop.

Note that this is just a label to mark the start of a block.

Check if i < arraySize

dup3 dup2 // [0, 96, 0, 0] 0x20 mul // [0*32, 96, 0, 96] lt iszero end jumpi // [0 < 96, 0, 0, 96]

Duplicates the i and arrayLength values, multiplies i by 32, and checks whether i*32 is less than arrayLength. If it's not, it jumps to the end label to terminate the loop. We multiply index i with 32 because each element is 32 bytes. So in 2nd iteration, i will be 1 and we check 1_32 < 96 true, then continue. Next iteration, i_32 will be 64 so iteration still continues. When its 4th iteration, i will be 3 so i*32 will be 96 which is not less than 96 so the control jumps to the end block .

Accessing Array Elements

dup1 0x20 mul // [0*32, 0, 0, 96] 0x44 add // [0*32 + 68, 0, 0, 96] calldataload // [arr[i]:1, 0, 0, 96]

Calculates the offset to access the i-th element from calldata and loads it onto the stack. calldataload is an opcode that takes in offset as input and loads 32-byte value starting from the given offset. So in out case the offset is 68, so calldataload will copy 32 bytes from byte 69.

0x1e2aea0600000000000000000000000000000000000000000000000000000000000000200000000000000000000000000000000000000000000000000000000000000003_**0000000000000000000000000000000000000000000000000000000000000001**_00000000000000000000000000000000000000000000000000000000000000030000000000000000000000000000000000000000000000000000000000000005

So in the first iteration 0x1 (left padded) will be copied to the stack. In the next iteration, 3 will be copied and in the final iteration 5 will be copied to the stack.

Update Sum

dup3 // [sum:0, arr[i]:1, i:0, sum:0, arrayLength:96] add // [sum + arr[i]:1, i:0, oldSum:0, arrayLength:96] swap2 pop // [i:0, newSum:1, arrayLength:96]

Here, we bring the sum to top of the stack and add with arr[i] to calculate the new sum. Then once the new sum is calculated, swap the new sum with the old sum and pop the old sum from the stack.

Increment Index

0x1 add // [i++, newSum:1, arraylength:96] loopBegin jump // Jump to loopBegin label

Increments i by 1 and jumps back to loopBegin for the next iteration. So this process continues till index value is 3. When i=3, the array index check fails, as 3*32 is not less than 96. Hence the control will be transferred to the end block:

Loop End

/// Stack: [index, finalSum, arrayLength] end: pop // [finalSum, arrayLength] : pops index out of stack push0 mstore // [arrayLength] : store final sum in memory 0x20 push0 return // Return the sum of the array from memory

Pops the remaining index from the stack and stores the final sum at memory location 0. Then returns 32 bytes starting from memory location 0, which contains the final sum.

Note: The above example is not most optimized and there are no safety checks like overflow protection. The goal of this post is to help developers understand the basics of Huff actually by writing a contract. Hence it should not be used in production.

If you've followed along this far, kudos to you! 🥳🎉 Even though we cannot cover the entire under-the-hood topics in a single post, I tried to cover most of the important details. So feel free to read it multiple times until you fully understand it at your own pace.

Gas comparison

I quickly ran a quick comparison of gas consumption for both the implementations. Here are the results:

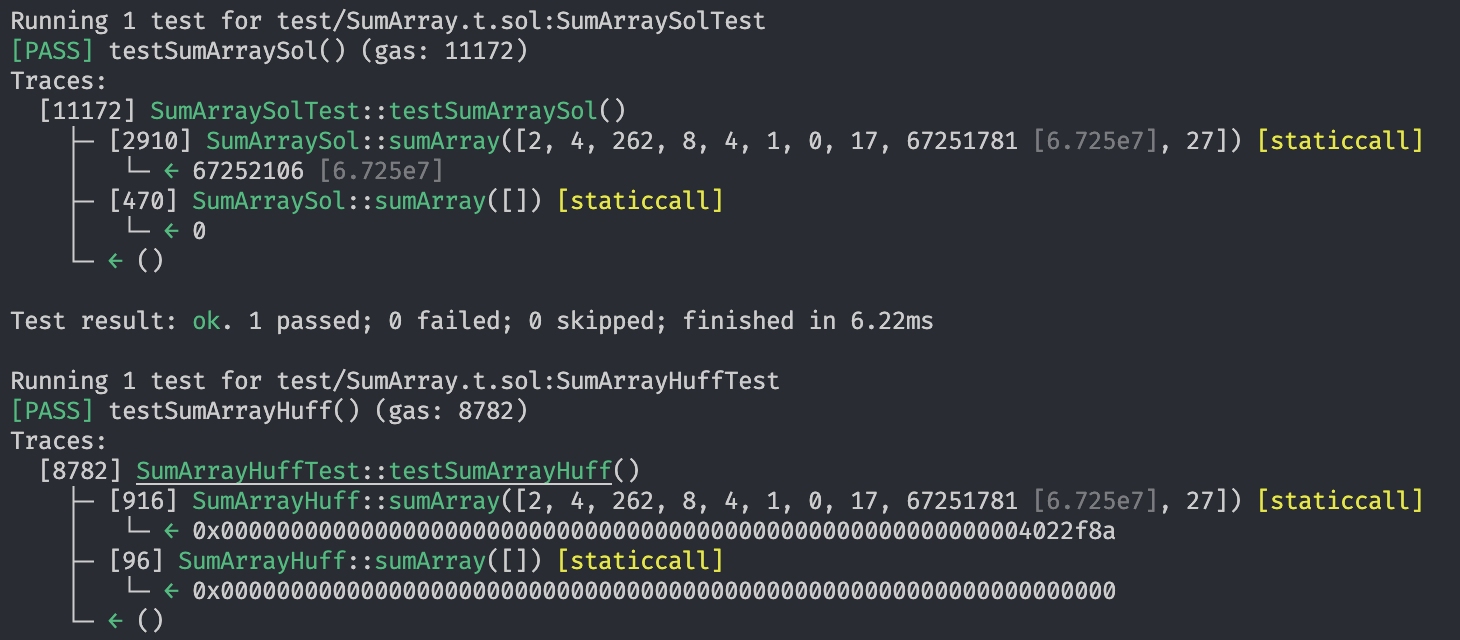
You can see that SumArrayHuff::sumArray() call costs 916 gas whereas SumArraySol::sumArray() costs around 2910 gas which is like ~3x more than that of Huff.

Conclusion:

Huff may seem intimidating at first glance, but it offers an unparalleled level of control and optimization. Being mindful of gas costs and storage operations can make your smart contracts perform better and cost less. This example illustrates how fundamental operations like summing an array can be optimized for gas consumption.

“With great power comes great responsibility“

Since Huff grants you the power of complete access to stack and opcodes, the developers should be super careful and should be aware of what they implement.

1. Huff can be gas-efficient but a tiny mistake can cost a lot. Always test thoroughly.

2. Huff and inline assembly don't have the rich debugging tools that higher-level languages offer. You'll need to be extra careful.

By diving into Huff, you'll understand what happens under the hood, so you’d be better equipped to write more efficient, cost-effective smart contracts. Until the next time, keep coding and stay curious! 🚀