Merkle and Verkle trees

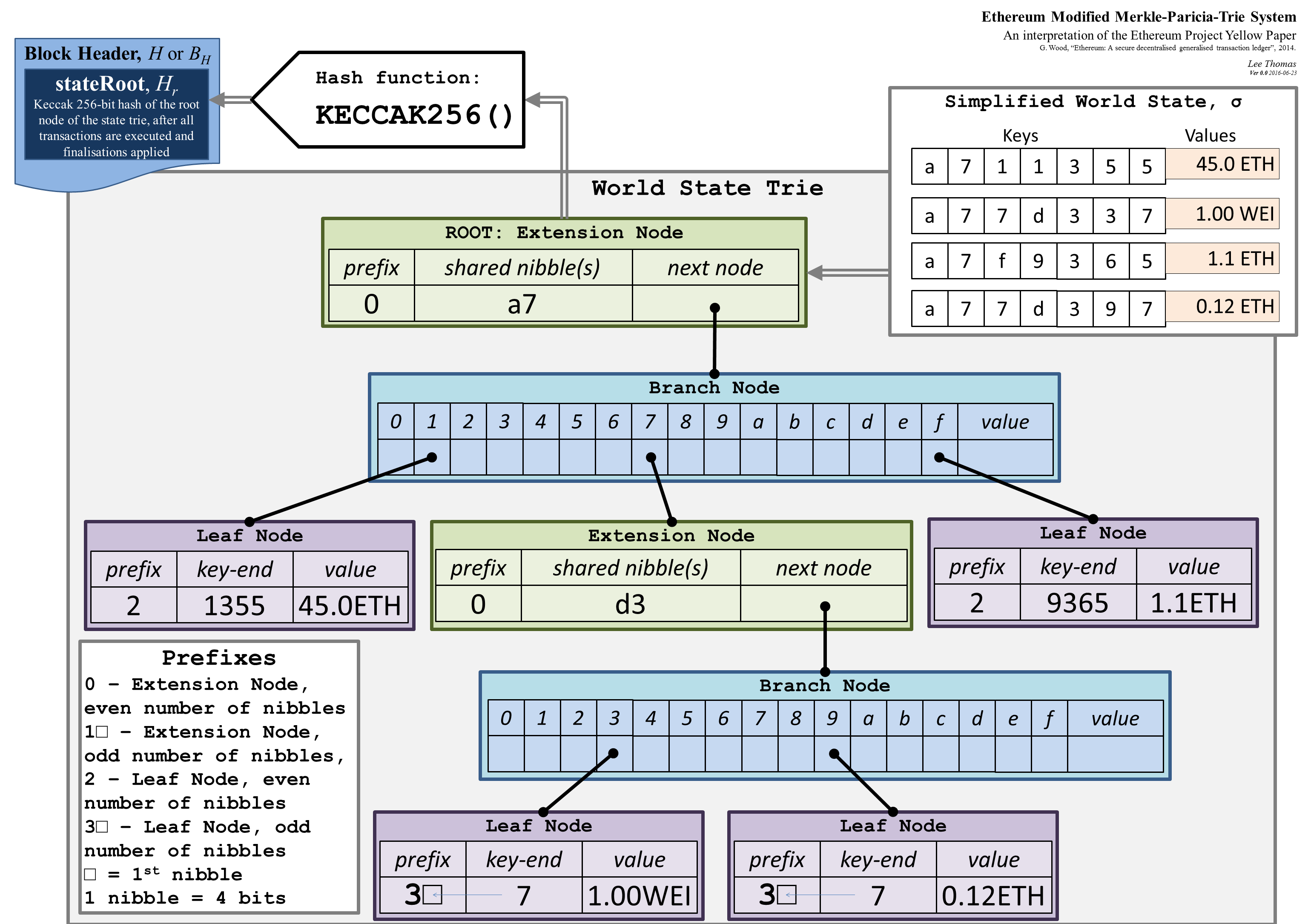
Merkle Practicia Trie

In general, data structures are used to efficiently store and retrieve data. In the world of blockchain, merkle trees are quite popular as it is being used in bitcoin and in the ethereum blockchain to store and verify the state (Modified Merkle Patricia Trie - Fig1). Now-a-days the merkle proofs are being utilized for various usecases like whitelisting address for token airdrops, NFT minting and so on...

What are Merke trees?

In a nutshell, a merkle tree is a tree data structure in which all the non-leaf nodes are the hash (sha256) of its child nodes. It is constructed by recursively hashing all the nodes until only one node is left which is called the merkle root. Every node is either (i) empty, (ii) a leaf node containing a key and value, or (iii) an intermediate node that has some fixed number of children (the "width" of the tree). The value of an intermediate node is computed as a hash of the values of its children.Merkle Trees are computationally fast, and a Merkle Tree over n nodes can be constructed in O(n) time.

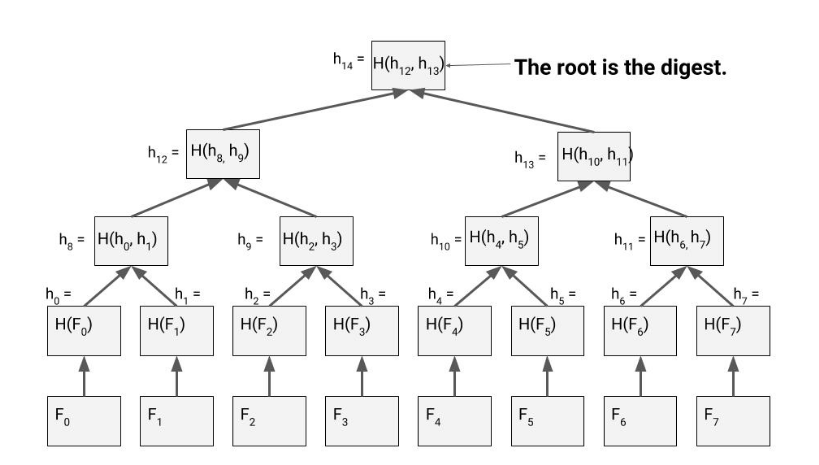
Binary Merkle Tree (Fig-2)

Use cases

Consensus Protocols
Public-Key Directories
Cryptocurrencies
Encrypted Web Applications
Secure File Systems

Verification of merkle proof

Consider Fig-2 as a file storage system, and we need to validate the file F3 returned by the file system (fs from now on) is valid. So in-order to compute the proof, the fs sends the following nodes along with the file F3.

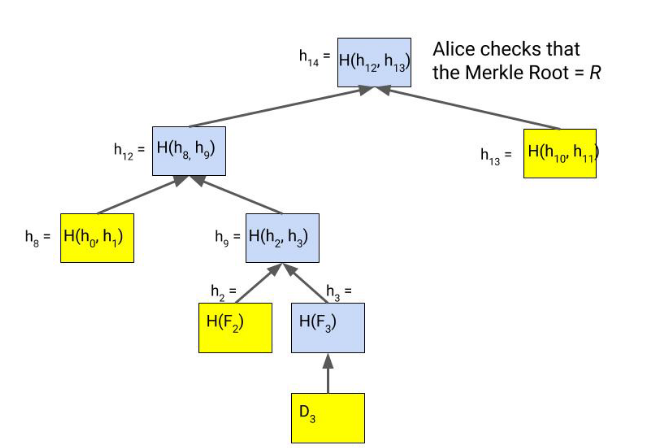
The Merkle Proof (in yellow)

The problem here is, the size of the merkle proof is directly proportional to the number of nodes. If Alice has around 1 billion files (2³⁰), the depth of the tree will be around 30. The proof size will be around 1KB. hence the Merkle Proof itself could create a large and expensive bandwidth overhead.

To overcome this issue, one can introduce a k-ary Merkle tree where k ( > 2 ) is the branching factory to reduce the depth of the tree. Giving our Merkle tree a branching factor of k reduces the height of the tree, unfortunately, the Merkle proof actually grows larger, from O(log₂ n) to O(k log_k n)

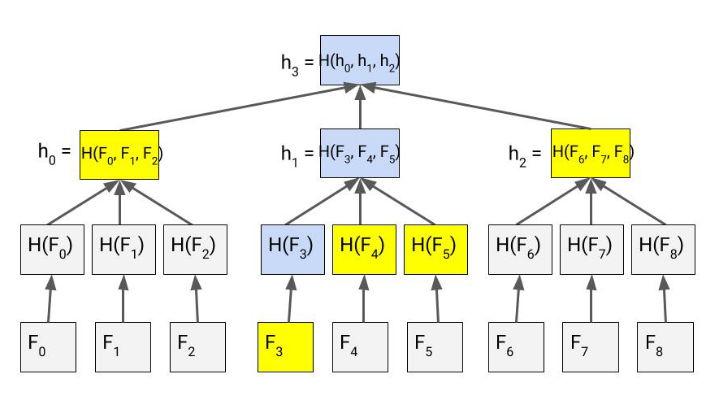
A 3-ary Merkle Tree

Verkle trees

Verkle trees are similar to merkle trees with a difference that the hash function is replaced by Vector commitments.

According to Vitalik, a vector commitment scheme is a special type of hash function, hashing a list

h (z_{1}, z_{2} . . . z_{n}) \to C

But vector commitments have the special property that for a commitment C and a value z_i, it's possible to make a short proof that is the commitment to some list where the value at the i'th position is z_i. In a Verkle proof, this short proof replaces the function of the sister nodes in a Merkle Patricia proof, giving the verifier confidence that a child node really is the child at the given position of its parent node.

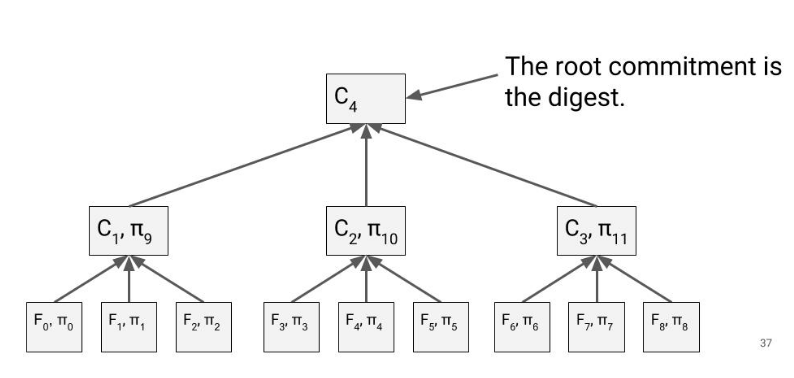
Verkle Tree

Comparision:

Operation	Construction	Proof size
Merkle Tree	O(n)	O(log₂n)
k-ary Merkle Tree	O(n)	O(klog_kn)
(k-ary) Verkle Tree	O(kn)	O(log_kn)

Conclusion

Verkle trees are efficient than merkle trees as they eliminate the need of siblings for proof calculation. Though they are cryptographically complex to implement, it faciliates improvements in ZK-SNARKs, ethereum scaling and more...